このページでは統計の基本となる標準正規分布(Z分布)について全部で2つのモジュールで取り扱っていきます。

今回は標準正規分布(Z分布)をPythonで取り扱う方法を知りたいです!
標準正規分布を取り扱うにはどういった方法があるんですか?

numpyやscipyといった科学技術計算を行うためのライブラリで扱うことができます!
今回は標準正規分布に従うデータを生成する方法を勉強していきましょう!
標準正規分布(Z分布)は、平均(μ)が0、標準偏差(σ)が1の正規分布です。
通常、標準正規分布を表すときは、Zという記号を使用します。
以下では、それぞれのライブラリの使い方を例とともに説明します。
標準正規分布に従うデータを生成する2つの方法
Pythonで標準正規分布に従うデータを生成する方法は2つあります。
- numpy.random.normal()関数でデータ生成する方法
- scipy.stats.normモジュールでデータ生成する方法
生成したデータを元にグラフの描画も行います。それぞれ順番に説明していきます。
numpy.random.normal()関数でデータ生成する方法
numpyは科学計算を行うためのライブラリで、正規分布からランダムな値を生成するnumpy.random.normal()関数を提供しています。
import numpy as np
import matplotlib.pyplot as plt
# 平均μ=0,標準偏差σ=1
mu, sigma = 0, 1
# 標準正規分布に従うランダムな値を1000件生成
s = np.random.normal(mu, sigma, 1000)
#ヒストグラムで表示
plt.hist(s)
plt.show()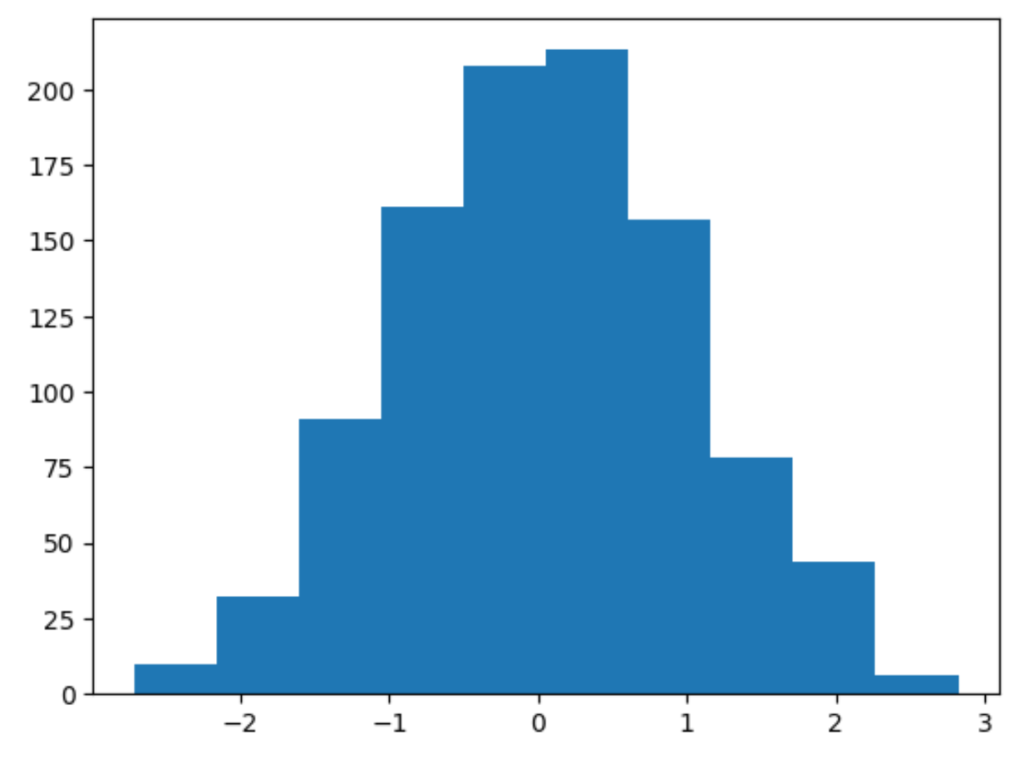
scipy.stats.normモジュールでデータ生成する方法
scipyは科学技術計算を行うためのライブラリで、正規分布を扱うためのscipy.stats.normモジュールを提供しています。
このモジュールには、正規分布に関連する様々な関数が含まれています。
例えば、rvs()関数を使ってランダムな値を生成したり、pdf()関数を使って確率密度関数を計算したり、cdf()関数を使って累積分布関数を計算したりできます。
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
# 平均μ=0,標準偏差σ=1
mu, sigma = 0, 1
# 確率密度関数
x = np.linspace(norm.ppf(0.01), norm.ppf(0.99), 100)
pdf = norm.pdf(x, mu, sigma)
# 標準正規分布に従うランダムな値を1000件生成
s = norm.rvs(mu, sigma, size=1000)
#ヒストグラムで表示
plt.hist(s)
plt.show()
正規分布の標準化をやってみよう!
それでは、先ほど用いたscipy.stats.normモジュールを用いて、正規分布を標準正規分布に変換(標準化)してみましょう!
正規分布の確率密度関数のグラフと標準化した標準正規分布確率密度関数のグラフを表示してみます。
まずは元になる平均μ=50,標準偏差σ=10の確率密度関数を表示してみます。
#平均μ=50,標準偏差σ=10の確率密度関数を表示
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
# 平均μ=50,標準偏差σ=10
mu, sigma = 50, 10
# 描画する確率変数xの範囲を指定
x = np.linspace(0, 100, 1000)
# 平均μ=50,標準偏差σ=10の正規分布の確率密度関数
pdf = norm.pdf(x, mu, sigma)
#確率密度関数をプロット表示
plt.plot(x, pdf)
plt.grid()
plt.show()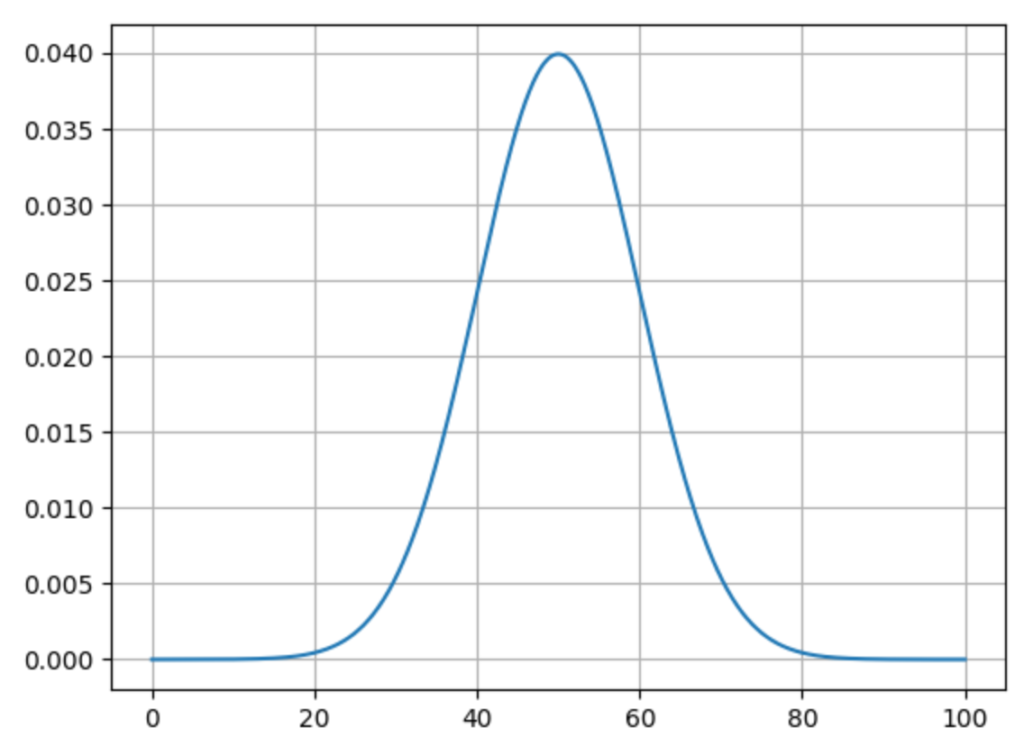
このプログラムを基に標準化を行ってみます!
標準化した標準正規分布確率密度関数のグラフを表示してみましょう。
#正規分布を標準化
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
# 平均μ=50,標準偏差σ=10
mu, sigma = 50, 10
# 描画する確率変数xの範囲を指定
x = np.linspace(0, 100, 1000)
#標準化 Z = x-μ/σ
z = (x - mu)/sigma
# 標準化した正規分布の確率密度関数
pdf = norm.pdf(z, 0, 1)
#確率密度関数をプロット表示
plt.plot(z, pdf)
plt.grid()
plt.show()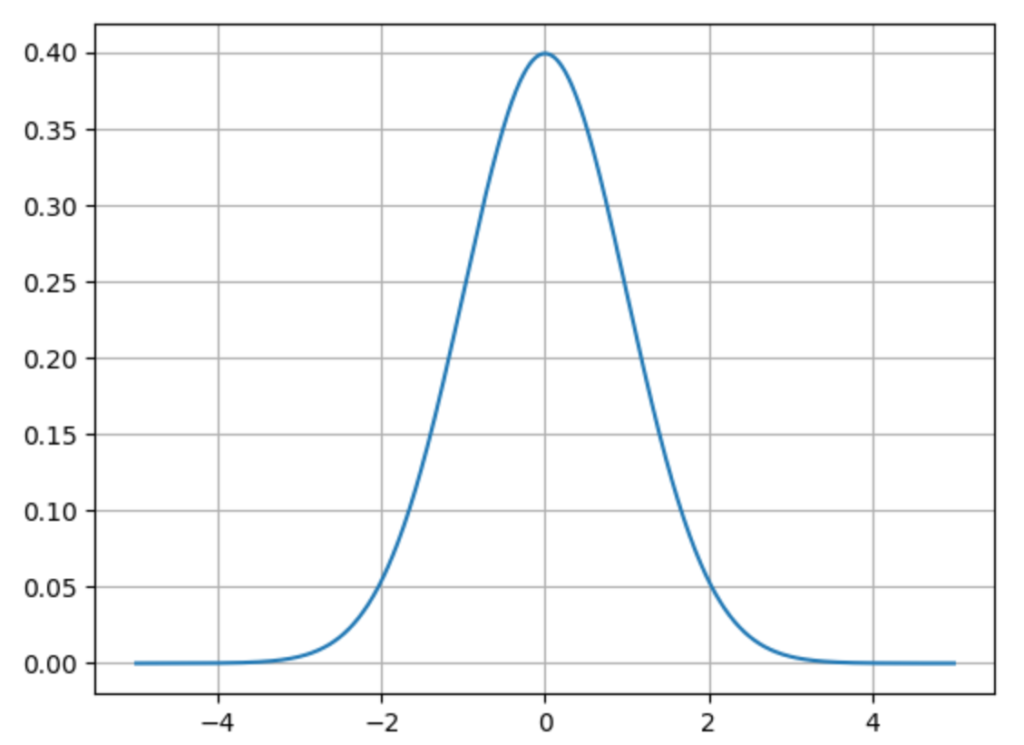
グラフの通り、標準正規分布の形がグラフとして確認できましたね!

平均0、標準偏差1の標準正規分布を自在に扱えるようになってきました!
numpyとscipyを用いる2種類の方法で標準正規分布を取り扱えるんですね!

numpyとscipy、とっても便利ですね!
最後に紹介した正規分布の標準化は統計学を学ぶ上では良く用いる手法なのでPythonでも実行できるようにしておきたいですね!
まとめ
この記事では、Pythonで標準正規分布に従うデータを生成する方法について2つの方法を紹介しました。
どちらの方法も、生成したデータを元にヒストグラムを描画することで、正規分布の形状を確認することができます。
また、scipy.stats.normモジュールでは、確率密度関数や累積分布関数を計算する関数も提供されています。
今回は正規分布の標準化を行い、確率密度関数のグラフを確認しました。
どちらの方法もプログラム自体は簡単で使いやすいので、目的に合わせて使い分けてみてください!
このサイトの記事一覧へは以下へアクセス!






コメント