統計の基本となる基本統計量となる平均・中央値・最頻値について学んでいきましょう。
そもそも平均・中央値・最頻値とはなんでしょうか。

平均は生活のなかでもよく使います。
「1組の算数のテストの平均点は52点でした。」みたいに会話でも普通に使いますね!
でも、ちゅうおうち?さいひんち?は聞いたこともないです..

平均以外は聞きなじみがないかもしれませんね。
それでは平均・中央値・最頻値についてそれぞれ解説していきます!
まずは平均について教えていきます。
平均 (平均値)とは
平均(平均値)とは複数の数値において、それぞれの値を全て足し合わせて、数値の個数で割った値のことです。
数式で表すと以下のようになります。
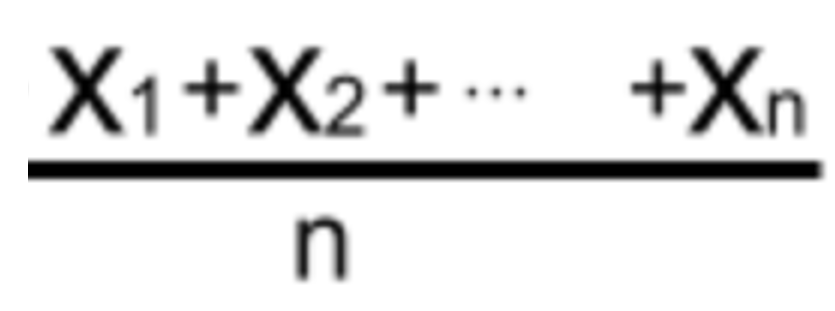
ただし、X1,X2,・・・Xnはそれぞれの数値、nは数値の個数を表します。
以下の表で実際に平均値を計算してみましょう。

この表は「ごまこのクラスの算数のテストの点数」です。
ごまこのクラスの算数のテストについて、点数の平均は以下のようになります。
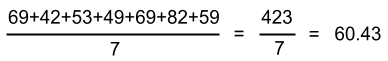

数式で書くと難しそうだけど、実際に計算してみると簡単ですね。

意外と簡単にできましたよね。
数式だと難しく感じるけど、実際に計算してみると理解しやすいし、数式にも慣れていきます!
実際に手で書いたりしながら慣れていくのが良いと思います。
続けて、中央値についても解説していきます!
中央値とは
中央値とは、データを小さい順・大きい順に並び替えた時にちょうど真ん中にある値のことです。
さきほどの「ごまこのクラスの算数のテストの点数表」で実際に中央値を求めてみましょう。

まず、上の表「ごまこのクラスの算数のテストの点数表」を点数の小さい順(昇順)に並べ替えます。

上の表から小さい順に並び替えた時に真ん中になる値は「59点」となります。

私も中央値を求めることができました。
でもクラスで7匹で奇数だから真ん中の中央値が求められましたが、偶数の場合中央値はどうやって求めるんですか?

いいところに気がつきましたね。
それでは実際にぼくのクラスのテスト結果で中央値を求めてみましょう。
僕のクラスは全部で8匹、つまり偶数のアザラシがいます!
下の表は「ごまおのクラスの算数のテストの点数」を小さい順(昇順)に並べ替えたものです。

この場合、真ん中にある値は上の表のように「ごままとごまんさ」の二つの値の間にあります。
このため、値(データ)が偶数の場合は真ん中の二つの値の平均値が中央値となります。つまりこの場合の中央値は以下のようになります。
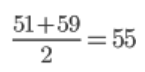

真ん中にいる「ごままの点数」と「ごまんさの点数」を足して2で割ると求められるんですね。

その通りです!
データ(値)の数が奇数か偶数かによって求め方が変わるので注意してくださいね。
最後に最頻値について解説していきます!
最頻値とは
最頻値とはデータの中で一番多く現れる値、最も頻度が高い値のことです。
これまでに紹介した「ごまこ・ごまおのクラスの算数の点数表」でそれぞれ最頻値を求めてみましょう。
まず、「ごまこのクラスの算数の点数表」を小さい順(昇順)に並び替えると以下のようになります。

この表から、
○「ごまこ・ごまごまー」は69点 で同じデータが2つ
○他のデータは全て異なる値のデータで1つずつ(同じものはない)
ということが分かります。
よって、データの中で一番多く現れる値、最も頻度が高い値は「ごまこ・ごまごまー」の点数69点となります。
同様に「ごまおのクラスの算数の点数表」を小さい順(昇順)に並び替えると以下のようになります。

この表から、
○「ごまじ・ごまや・ごまさ」は43点 で同じデータが3つ
○他のデータは全て異なる値のデータで1つずつ(同じものはない)
ということが分かります。
よって、データの中で一番多く現れる値、最も頻度が高い値は「ごまじ・ごまや・ごまさ」の点数43点となります。

一番多く出てくるデータが最頻値なんですね!

理解してもらえたようで良かったです。
あと今回求めた「ごまこのクラスの算数の点数」の平均値、中央値、最頻値はそれぞれ60.43点 、59点 、69点と異なる値になっていることにも注目しておいてほしいです。
まとめ
今回は統計学を学ぶ上で基本となる平均・中央値・最頻値を学びました。
統計初心者だと平均については知っていたけれど、中央値・最頻値は知らない、違いが分からないといった方もいたのではないかと思います。
統計の議論を進めていく上で、平均・中央値・最頻値は基本の基本になりますのできちんと意味を理解していただければと思います。
さらに統計について学びたいという方は以下の分散・標準偏差についての記事もご覧ください。
また、いま良く使われているPythonというプログラミング言語を使って、平均・中央値・最頻値を求めてみたい方は以下の記事も見てください!
このサイトの記事一覧へは以下へアクセス!







達人に学ぶDB設計 徹底指南書