このページでは統計の基本となる二項分布について全部で2つのモジュールで取り扱っていきます。

今日はPythonで二項分布を扱う方法を知りたいんです!
二項分布を取り扱うためのモジュールはどういったものがあるんですか?

みなさんがよく知っているnumpyやscipyなどの科学技術計算を行うためのライブラリでも扱うことができます!
今回は二項分布に従うデータを生成する方法を勉強していきましょう!
二項分布とは、ある試行を n 回行った時に、成功する回数が X 回となる確率分布のことです。
また、Xが二項分布に従うとき、試行回数nや1回の成功確率pは確率分布を特徴づける値となります。
Pythonでは、さまざまなライブラリを使って、簡単に二項分布に従うデータを生成することができます。
以下では、それぞれのライブラリの使い方を例とともに説明します。
二項分布に従うデータを生成する2つの方法
Pythonで二項分布に従うデータを生成する方法は2つあります。
- numpy.random.binomial関数でデータ生成する方法
- scipy.stats.binomモジュールでデータ生成する方法
生成したデータを元にグラフの描画も行います。それぞれ順番に説明していきます。
numpy.random.binomial関数でデータ生成する方法
numpyは科学計算を行うためのライブラリで、二項分布からランダムな値を生成するnumpy.random.binomial()関数を提供しています。
import numpy as np
import matplotlib.pyplot as plt
# 試行回数nと確率p
n, p = 100, 0.5
# n回の試行を1000回繰り返した場合の
# それぞれの成功回数s
s = np.random.binomial(n, p, 1000)
#ヒストグラムを描画
plt.hist(s)
plt.show()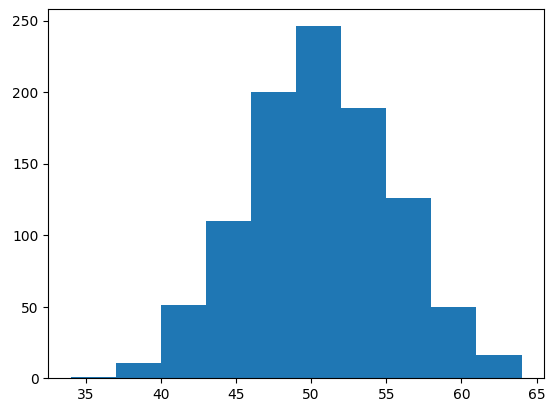
scipy.stats.binomモジュールでデータ生成する方法
scipyは科学技術計算を行うためのライブラリで、二項分布を扱うためのscipy.stats.binomモジュールを提供しています。
このモジュールには、二項分布に関連する様々な関数が含まれています。
例えば、rvs()関数を使ってランダムな値を生成したり、pmf()関数を使って確率質量関数を計算したり、cdf()関数を使って累積分布関数を計算したりできます。
from scipy.stats import binom
import matplotlib.pyplot as plt
# 試行回数nと確率p
n, p = 100, 0.3
# 確率質量関数
x = range(n+1)
pmf = binom.pmf(x, n, p)
# n回の試行を1000回繰り返した場合の
# それぞれの成功回数s
s = binom.rvs(n, p, size=1000)
#ヒストグラムを描画
plt.hist(s)
plt.show()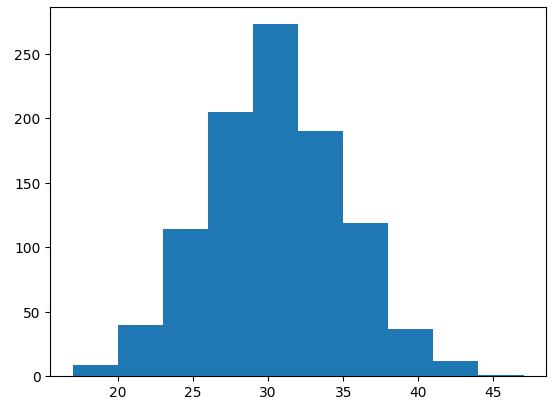

離散型の二項分布を表示できました~!
二項分布を表示するだけでもいろいろな方法があるんですね!

今回グラフの表示にはmatplotlibを用いましたが、seabornなど他のグラフ描画モジュールもありますね!
詳細なグラフの設定を含めて目的に合わせて使い分けられると良いと思います!
まとめ
この記事では、Pythonで二項分布に従うデータを生成する方法について2つの方法を紹介しました。
どちらの方法も、生成したデータを元にヒストグラムを描画することで、二項分布の形状を確認することができます。
また、scipy.stats.binomモジュールでは、確率質量関数や累積分布関数を計算する関数も提供されています。
これらの関数を使って、二項分布の特徴を詳しく調べることもできます。
どちらの方法もプログラム自体は簡単で使いやすいので、目的に合わせて使い分けてみてください!
このサイトの記事一覧へは以下へアクセス!






コメント